Convolutional neural networks (CNN) Deep Learning - Part 3
Contributors
Questions
What is a convolutional neural network (CNN)?
What are some applications of CNN?
Objectives
Understand the inspiration behind CNN and learn the CNN architecture
Learn the convolution operation and its parameters
Learn how to create a CNN using Galaxy’s deep learning tools
Solve an image classification problem on MNIST digit classification dataset using CNN in Galaxy
Requirements
- tutorial Hands-on: Introduction to deep learning
- slides Slides: Deep Learning (Part 1) - Feedforward neural networks (FNN)
- tutorial Hands-on: Deep Learning (Part 1) - Feedforward neural networks (FNN)
- slides Slides: Deep Learning (Part 2) - Recurrent neural networks (RNN)
- tutorial Hands-on: Deep Learning (Part 2) - Recurrent neural networks (RNN)
last_modification Published: May 19, 2021
last_modification Last Updated: Jun 2, 2022
What is a convolutional neural network (CNN)?
Speaker Notes
What is a convolutional neural network (CNN)?
Convolutional Neural Network (CNN)
- Increasing popularity of social media in past decade
- Image and video processing tasks have become very important
- FNN could not scale up to image and video processing tasks
- CNN specifically tailored for image and video processing tasks
Feedforward neural networks (FNN)
- In FNN all nodes in a layer connected to all nodes in next layer
- Each connection has a weight, must be learned by learning algorithm
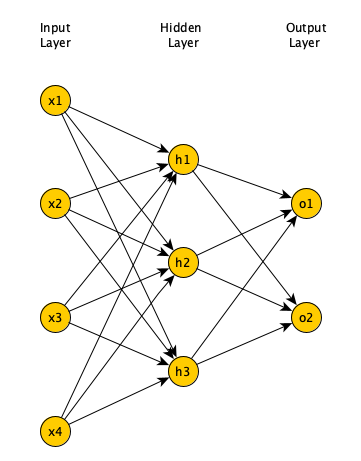
Limitations of FNN
- If input is 64 pixel by 64 pixel grayscale image
- Each grayscale pixel represented by 1 value, usually between 0 to 255
- Where 0 is black, 255 is white, and values in between are shades of gray
- Since each grayscale pixel represented by 1 value, we say channel size is 1
- Image represented by 64 x 64 x 1 = 4,096 values (rows x columns x channels)
- Hence, input layer of FNN has 4096 nodes
- Lets assume next layer has 500 nodes
- Since FNN fully connected, we have 4,096 x 500 = 2,048,000 weights
Limitations of FNN
- For complex problems, we need multiple hidden layers in our FNN
- Compunds the problem of having many weights
- Having too many weights
- Makes learning more difficult as dimension of search space is increased
- Makes training more time/resource consuming
- Increases the likelihood of overfitting
- Problem is further compunded for color images
- Each pixel in color image represented by 3 values (RGB color mode)
- Since each pixel represented by 3 values, we say channel size is 3
- Image represented by 64 x 64 x 3 = 12,288 values (rows x columns x channels)
- Number of weights is now 12,288 x 500 = 6,144,000
Limitations of FNN
- Clear that FNN cannot scale to larger images (Too many weights)
- Another problem with FNN
- 2D image represented as 1D vector in input layer
- Any spatial relationship in the data is ignored
Inspiration for CNN
- In 1959 Hubel & Wiesel did an experiment to understand how visual cortex of brain processes visual info
- Recorded activity of neurons in visual cortex of a cat
- While moving a bright line in front of the cat
- Some cells fired when bright line is shown at a particular angle/location
- Called these simple cells
- Other cells fired when bright line was shown regardless of angle/location
- Seemed to detect movement
- Called these complex cells
- Seemed complex cells receive inputs from multiple simple cells
- Have an hierarchical structure
- Hubel and Wiesel won Noble prize in 1981
Inspiration for CNN
- Inspired by complex/simple cells, Fukushima proposed Neocognitron (1980)
- Hierarchical neural network used for handwritten Japanese character recognition
- First CNN, had its own training algorithm
- In 1989, LeCun proposed CNN that was trained by backpropagation
- CNN got popular when outperformed other models at ImageNet Challenge
- Competition in object classification/detection
- On hundreds of object categories and millions of images
- Run annually from 2010 to present
- Notable CNN architectures that won ImageNet challenge
- AlexNet (2012), ZFNet (2013), GoogLeNet & VGG (2014), ResNet (2015)
Architecture of CNN
- A typical CNN has 4 layers
- Input layer
- Convolution layer
- Pooling layer
- Fully connected layer
- We will explain a 2D CNN here
- Same concepts apply to a 1 (or 3) dimensional CNN
Input layer
- Example input a 28 pixel by 28 pixel grayscale image
- Unlike FNN, we do not “flatten” the input to a 1D vector
- Input is presented to network in 2D as 28 x 28 matrix
- This makes capturing spatial relationships easier
Convolution layer
- Composed of multiple filters (kernels)
- Filters for 2D image are also 2D
- Suppose we have a 3 by 3 filter (9 values in total)
- Values are randomly set to 0 or 1
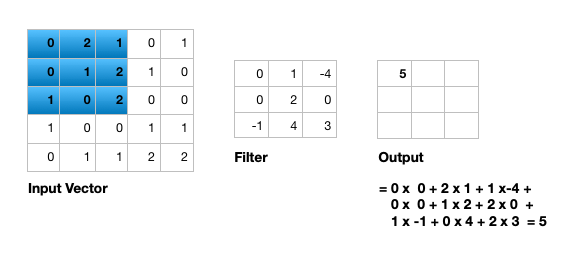
- Convolution: placing 3 by 3 filter on the top left corner of image
- Multiply filter values by pixel values, add the results
- Move filter to right one pixel at a time, and repeat this process
- When at top right corner, move filter down one pixel and repeat process
- Process ends when we get to bottom right corner of image
3 by 3 Filter
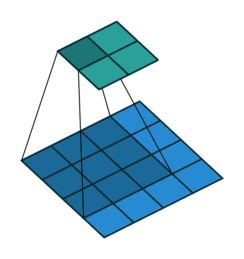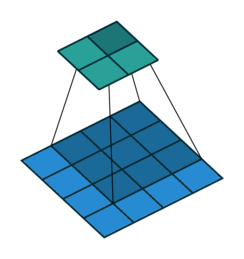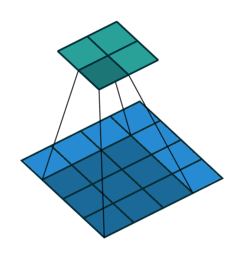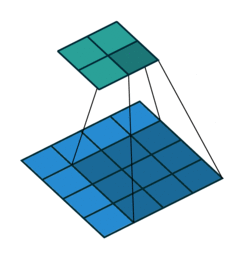
Convolution operator parameters
- Filter size
- Padding
- Stride
- Dilation
- Activation function
Filter size
- Filter size can be 5 by 5, 3 by 3, and so on
- Larger filter sizes should be avoided
- As learning algorithm needs to learn filter values (weights)
- Odd sized filters are preferred to even sized filters
- Nice geometric property of all input pixels being around output pixel
Padding
- After applying 3 by 3 filter to 4 by 4 image, we get a 2 by 2 image – Size of the image has gone down
- If we want to keep image size the same, we can use padding
- We pad input in every direction with 0’s before applying filter
- If padding is 1 by 1, then we add 1 zero in evey direction
- If padding is 2 by 2, then we add 2 zeros in every direction, and so on
3 by 3 filter with padding of 1
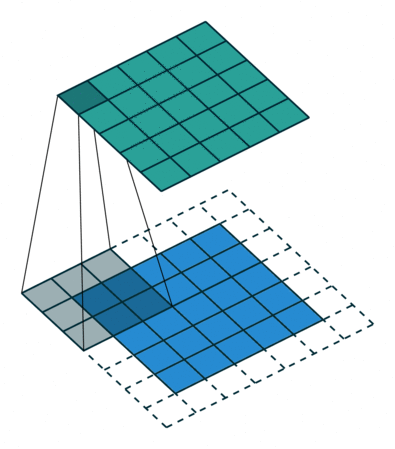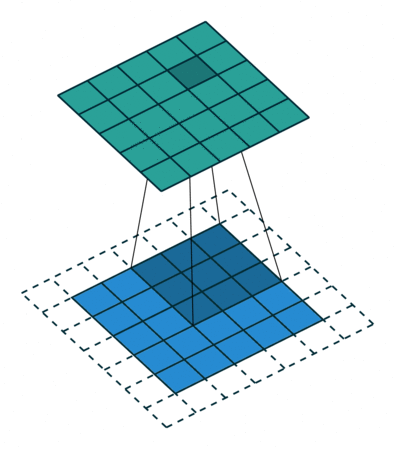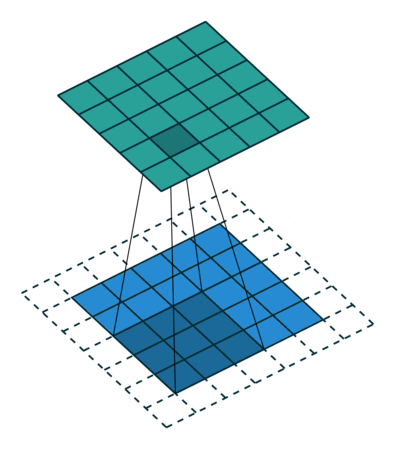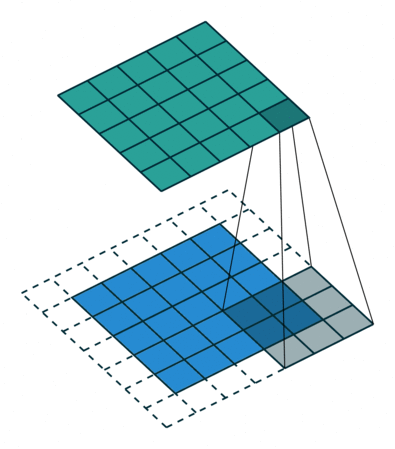
Stride
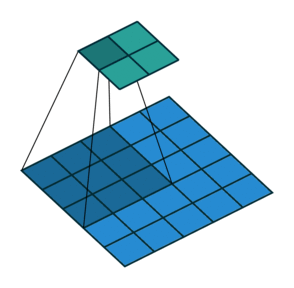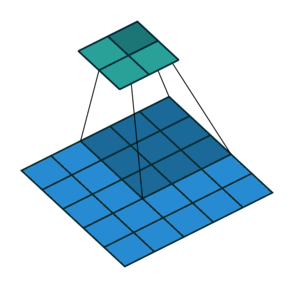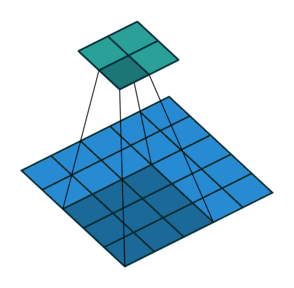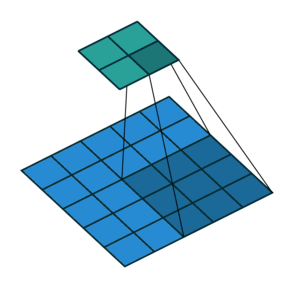
- How many pixels we move filter to the right/down is stride
- Stride 1: move filter one pixel to the right/down
- Stride 2: move filter two pixels to the right/down
3 by 3 filter with stride of 2
Dilation
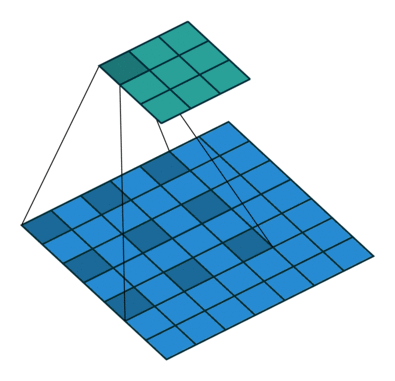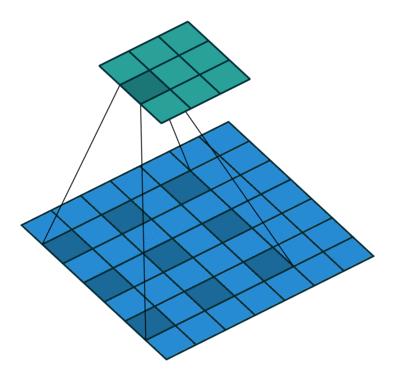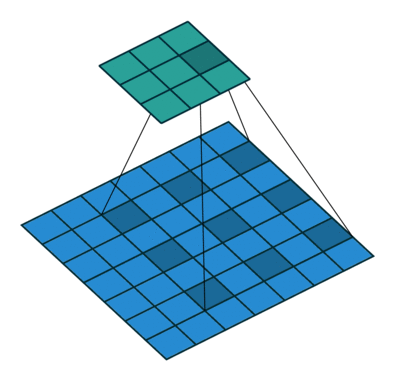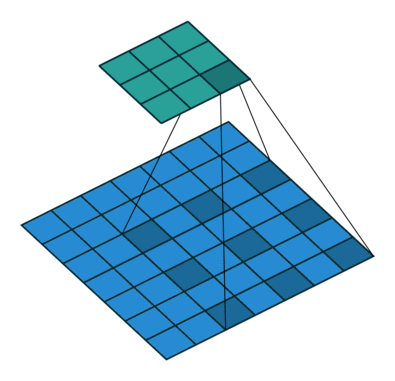
- When we apply 3 by 3 filter, output affected by pixels in 3 by 3 subset of image
- Dilation: To have a larger receptive field (portion of image affecting filter’s output)
- If dilation set to 2, instead of contiguous 3 by 3 subset of image, every other pixel of a 5 by 5 subset of image affects output
3 by 3 filter with dilation of 2
Activation function
- After filter applied to whole image, apply activation function to output to introduce non-linearlity
- Preferred activation function in CNN is ReLU
- ReLU leaves outputs with positive values as is, replaces negative values with 0
Relu activation function
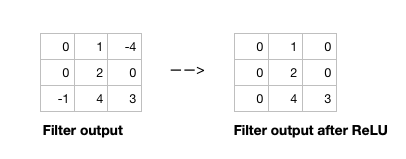
Single channel 2D convolution
Triple channel 2D convolution
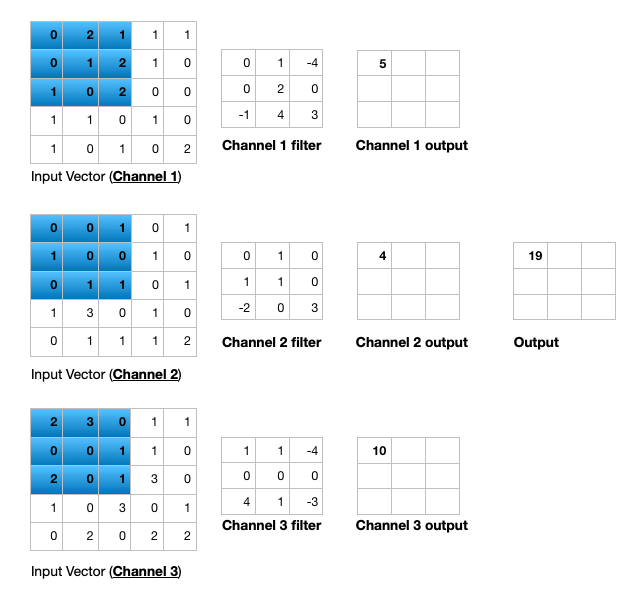
Triple channel 2D convolution in 3D
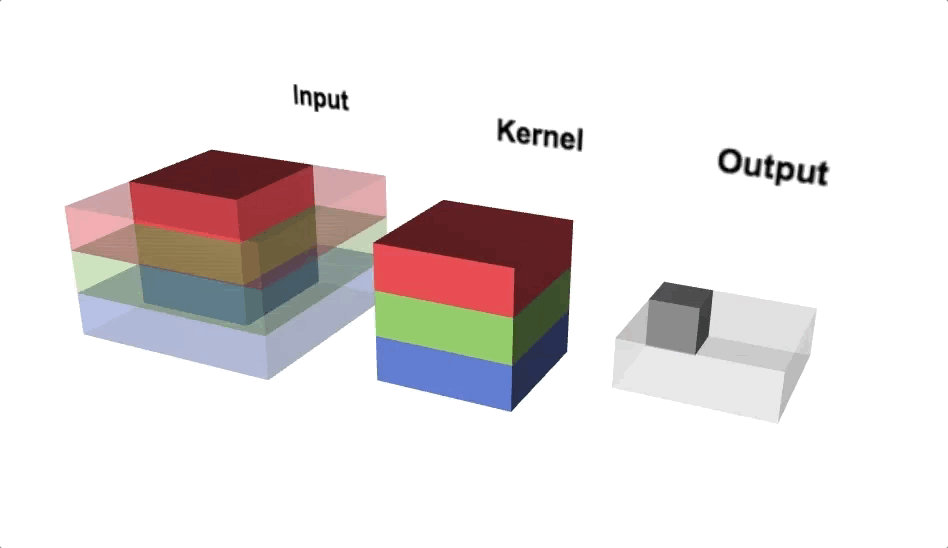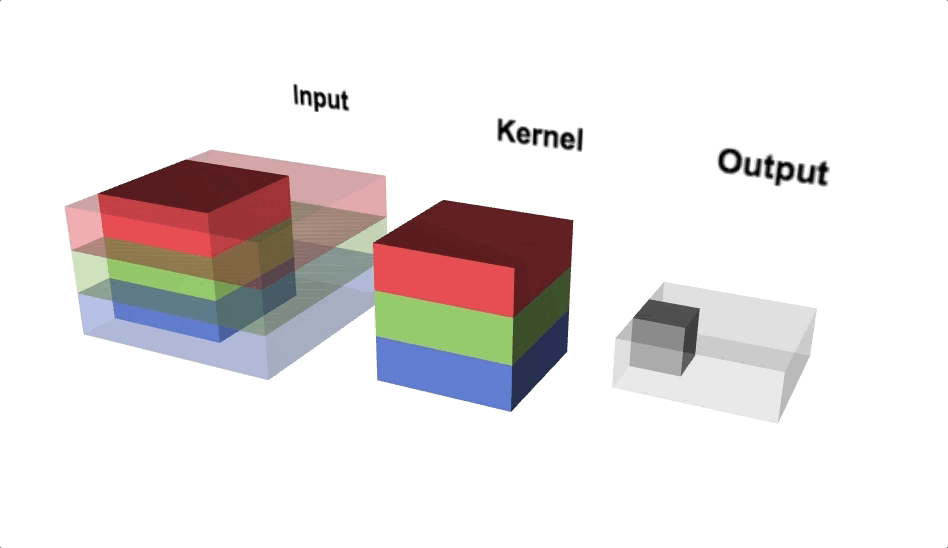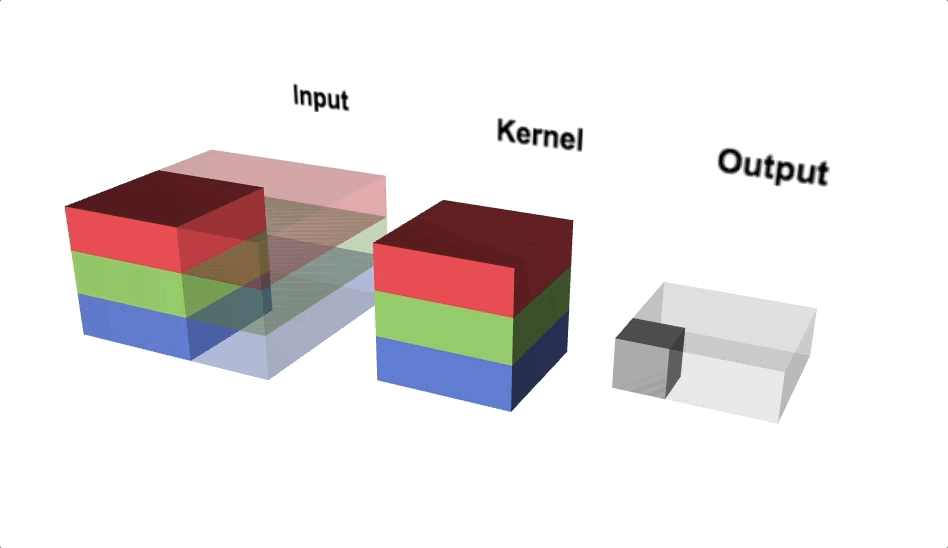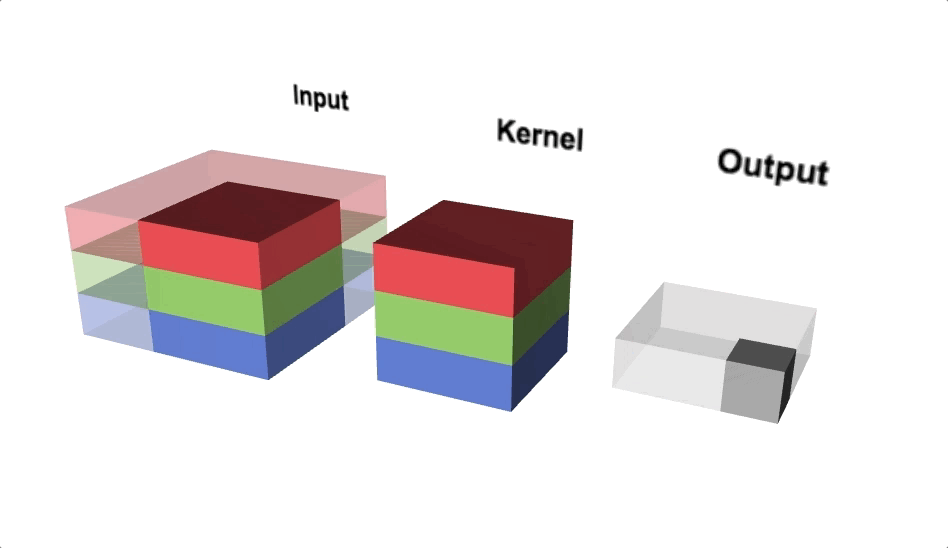
Change channel size
- Output of a multi-channel 2D filter is a single channel 2D image
- Applying multiple filters results in a multi-channel 2D image
- E.g., if input image is 28 x 28 x 3 (rows x columns x channels)
- We apply a 3 x 3 filter with 1 x 1 padding, we get a 28 x 28 x 1 image
- If we apply 15 such filters, we get a 28 x 28 x 15
- Number of filters allows us to increase or decrease channel size
Pooling layer
- Pooling layer performs down sampling to reduce spatial dimensionality of input
- This decreases number of parameters
- Reduces learning time/computation
- Reduces likelihood of overfitting
- Most popular type is max pooling
- Usually a 2 x 2 filter with a stride of 2
- Returns maximum value as it slides over input data
Fully connected layer
- Last layer in a CNN
- Connect all nodes from previous layer to this fully connected layer
- Which is responsible for classification of the image
An example CNN
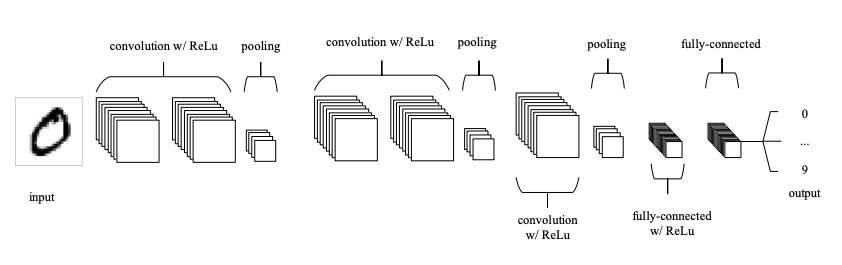
An example CNN
- A typical CNN has several convolution plus pooling layers
- Each responsible for feature extraction at different levels of abstraction
- E.g., filters in first layer detect horizontal, vertical, and diagonal edges
- Filters in the next layer detect shapes
- Filters in the last layer detect collection of shapes
- Filter values randomly initialized, learned by learning algorithm
- CNN not only do classification, but can also automatically do feature extraction
- Distinguishes CNN from other classification techniques (like Support Vector Machines)
MNIST dataset
- MNIST dataset of handwritten digits
- Composed of training set of 60,000 and test set of 10,000 images
- Digits have been size-normalized/centered in a fixed-size image (28 by 28 pixels)
- Images are grayscale
- Each pixel is represented by a number between 0 and 255
- 0 for black, 255 for white, and other values for shades of gray
- MNIST dataset is a standard image classification dataset
-
Used to compare various Machine Learning techniques
-
Classification of MNIST images with CNN
- We define a CNN and train it using MNIST dataset training data
- Goal is to learn a model such that given image of a digit we predict the digit (0 to 9)
- We then evaluate the trained CNN on test dataset and plot the confusion matrix
For references, please see tutorial’s References section
- Galaxy Training Materials (training.galaxyproject.org)
Speaker Notes
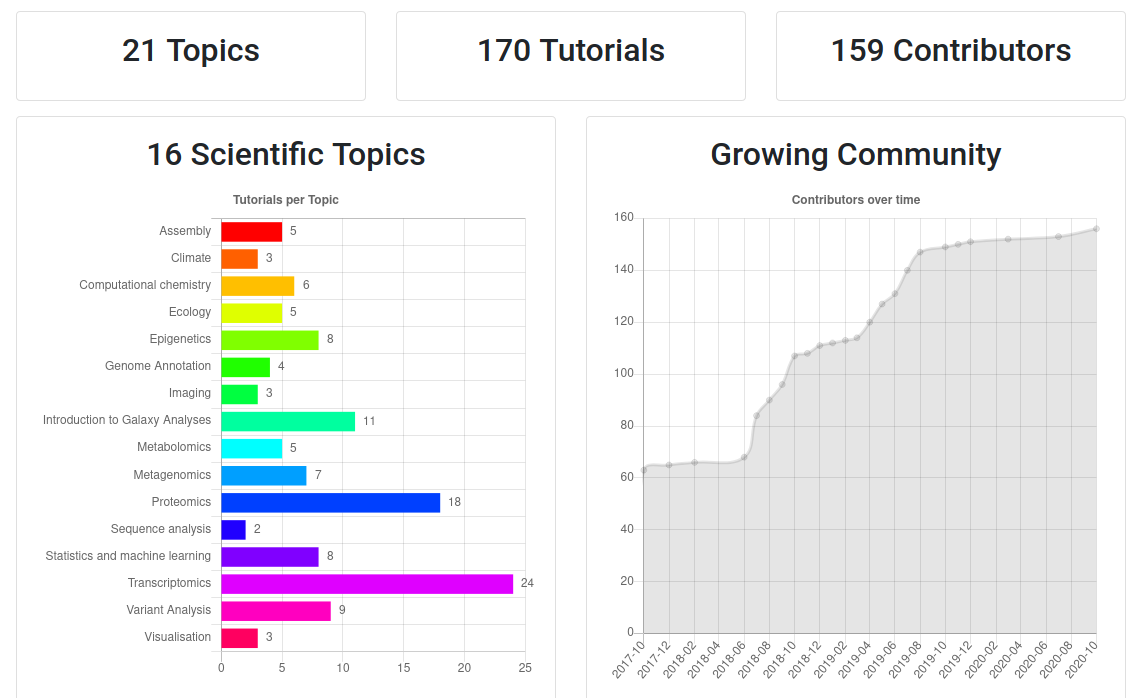
- If you would like to learn more about Galaxy, there are a large number of tutorials available.
- These tutorials cover a wide range of scientific domains.
Getting Help
-
Help Forum (help.galaxyproject.org)
-
Gitter Chat
- Main Chat
- Galaxy Training Chat
- Many more channels (scientific domains, developers, admins)
Speaker Notes
- If you get stuck, there are ways to get help.
- You can ask your questions on the help forum.
- Or you can chat with the community on Gitter.
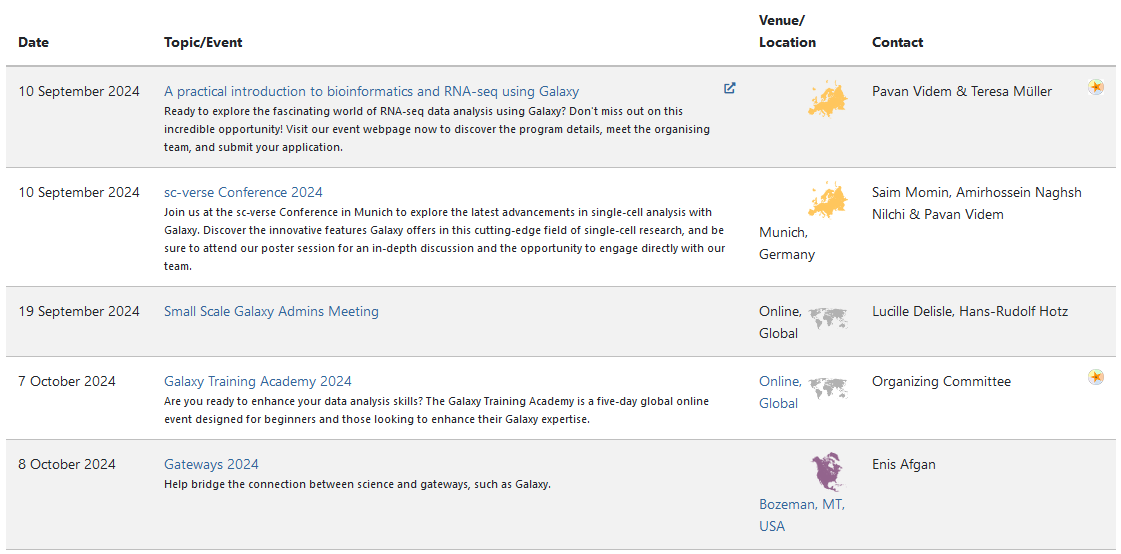
Join an event
- Many Galaxy events across the globe
- Event Horizon: galaxyproject.org/events
Speaker Notes
- There are frequent Galaxy events all around the world.
- You can find upcoming events on the Galaxy Event Horizon.
Thank you!
This material is the result of a collaborative work. Thanks to the Galaxy Training Network and all the contributors! Tutorial Content is licensed under
Creative Commons Attribution 4.0 International License.
Tutorial Content is licensed under
Creative Commons Attribution 4.0 International License.