Phylogenetics - Back to Basics

name: inverse
layout: true
class: center, middle, inverse

</div>

</div>

---

# Phylogenetics - Back to Basics - Building Trees

<div class="contributors-line">
		<a href="/training-material/hall-of-fame/mcharleston/" class="contributor-badge contributor-mcharleston"><img src="https://avatars.githubusercontent.com/mcharleston?s=36" alt="Michael Charleston avatar" width="36" class="avatar" />
 Michael Charleston</a>
	</div>

</div>

<div class="footnote" style="bottom: 8em;">
 last_modification Updated:  
 purl<abbr title="Persistent URL">PURL</abbr>: <a href="https://gxy.io/GTN:S00121">gxy.io/GTN:S00121</a>
</div>

<div class="footnote" style="bottom: 5em;">

text-document<a href="slides-plain.html"> Plain-text slides</a> |

</div>

<div class="footnote" style="bottom: 2em;">
 Tip: press <kbd>P</kbd> to view the presenter notes
 | arrow-keys Use arrow keys to move between slides

</div>

???
Presenter notes contain extra information which might be useful if you intend to use these slides for teaching.

Press `P` again to switch presenter notes off

Press `C` to create a new window where the same presentation will be displayed.
This window is linked to the main window. Changing slides on one will cause the
slide to change on the other.

Useful when presenting.

---

## Requirements

Before diving into this slide deck, we recommend you to have a look at:

- [Introduction to Galaxy Analyses](/training-material/topics/introduction)

---

# Why _build_ trees?
 
The main reason we end up building a tree is that searching tree space for an optimal one takes too long when the number of taxa gets large.
 
.reduce70[
| _n_ | # trees | yes, but how much is that _really_?
| --- |---|:--|
| 3 | 3 | enumerable by hand |
| 4 | 15 | enumerable by hand |
| 5 | 105 | enumerable by hand on a rainy day |
| 6 | 945 | enumerable by computer |
| 7 | 10395 | still searchable very quickly on computer |
| 8 | 135135 | a bit more than the number of hairs on your head |
| 9 | 2027025 | population of Sydney living west of Parramatta |
| 10 | 34459425 | \$\approx\$ upper limit for exhaustive searching; about the number of possible combinations of numbers in the National Lottery |
| 20 | $$8.2\times 10^{21}$$ | \$ \approx \$ upper limit for branch-and-bound searching |
| 48 | $$ 3.21 \times 10^{70} $$ | \$\approx\$ number of particles in the universe |
| 136 | $$ 2.11 \times 10^{267} $$ | number of trees to choose from in the ``Out of Africa'' data¹ |
]

.footnote[
¹ Vigilant et al., 1991
]

---
# Tree space is worse than "space" space
 
![Hubble Space Telescope image of two colliding galaxies](graphics/NGC2207+IC2163.jpg)
 
NGC 2207 and IC 2163 galaxies colliding.
 
.footnote[Source: https://commons.wikimedia.org/wiki/Commons:Featured_pictures/Astronomy]
---
# Why should building work then?
 
 
Some parts of a phylogeny can be confidently accepted: when there are two species much more similar to each other than they are to any other species, we can confidently say that they are likely to be each other's closest relatives, in the set of species of interest.
 
 
If molecular sequences evolve at a nice steady rate - the "molecular clock" hypothesis - and if there's neither too little nor too much change, this can be good enough.

---
# Distances from trees
 
 
Before we talk about building a tree from distances, we need to think about how distances are reflected by trees.
 
 
The most natural way to infer distances from trees is by adding the lengths of branches between each pair of nodes.
 
 
Such distances are called *patristic* distances (I don't know why).
---
# Patristic Distances
 
 
![Schematic of a phylogenetic tree containing internal nodes a, b, c. Nodes d, e, f, g and h form the tips. The branches of the tree are annotated with numbers that represent the evolutionary distance between species. Described at 3:05 in the video recording.](graphics/04-NonUltrametricTree1-1.png)

Rooted binary tree with branch lengths
---
# Patristic Distances
 
 
![Schematic of a phylogenetic tree containing internal nodes a, b, c. Nodes d, e, f, g and h form the tips. The distance between nodes f and g via the internal node c is highlighted with a red dotted line and annotated with the value 0.045. Described at 3:50 in the video recording.](graphics/04-NonUltrametricTree2-1.png)
 
Patristic distance between tips f and g is 0.02 + 0.025 = 0.045
---
# Patristic Distances
 
 
![Schematic of a phylogenetic tree containing internal nodes a, b, c. Nodes d, e, f, g and h form the tips. The distance between nodes g and h via the internal nodes c and b is highlighted with a red dotted line and annotated with the value 0.07. Described at 4:03 in the video recording.](graphics/04-NonUltrametricTree3-1.png)
 
Patristic distance between tips g and h is 0.025 + 0.01 + 0.035 = 0.07
---
# Patristic Distances
 
 
![Schematic of a phylogenetic tree containing internal nodes a, b, c. Nodes d, e, f, g and h form the tips. The distance between nodes e and f the internal node a, the root and internal nodes b and c is highlighted with a red dotted line and annotated with the value 0.085.Described at 4:10 in the video recording.](graphics/04-NonUltrametricTree4-1.png)
 
Patristic distance between tips e and f is 0.02 + 0.015 + 0.02 + 0.01 + 0.02 = 0.085

---
# Tree-like distances are easy
 
 
A set of distances between the tips (taxa) that match the patristic distances of some tree is called **tree-like**.
 
 
Given tree-like distances, most tree construction methods will work.
 
 
Yes, _most_ - not all!

---

# Clock-like
 
 
The easiest possible distance data to work with are those where the distance from the root to every tip is the same.
 
 
Such trees (and the distances derived from them) are called _ultrametric_ (that is, they have the same root-to-tip distance for every tip).

---

# Clock-like
 
 
For example, suppose this is the _true_ tree relating some species of interest, with actual branch lengths as labelled:
 
 
![Schematic of a phylogenetic tree containing internal nodes a, b, c. Nodes d, e, f, g and h form the tips. The branches of the tree are annotated with numbers that represent the evolutionary distance between species. The distance between the root and tip on all branches is the same. Described at 4:44 in the video recording.](graphics/04-UltrametricTreeScaled-1.png)

---

# These distances are _ultrametric_
 
.pull-left[
.image-90[ ![Schematic of a phylogenetic tree containing internal nodes a, b, c. Nodes d, e, f, g and h form the tips. The branches of the tree are annotated with numbers that represent the evolutionary distance between species. The distance between the root and tip on all branches is the same. Described at 4:44 in the video recording.](graphics/04-UltrametricTree-1.png) ]
]
.pull.right[
* The maximum root-to-tip distance is called the _height_ of the tree.
* Here, the root-to-tip distances are all the same. A set of distances with this property is called _ultrametric_.
* If the distances represent evolutionary time accurately and all the tips are in the present, then we should expect this property.
* Reconstructing trees from ultrametric distances is _super easy_.
]
---

# These distances are _ultrametric_
 
 
.left-column40[
	![Schematic of a phylogenetic tree containing internal nodes a, b, c. Nodes d, e, f, g and h form the tips. The branches of the tree are annotated with numbers that represent the evolutionary distance between species. The distance between the root and tip on all branches is the same. Described at 4:44 in the video recording.](graphics/04-UltrametricTree-1.png)
]
.right-column60[
Distance matrix:
.center[
| | d | e | f | g | h |
|:---:|:---:|:---:|:---:|:---:|:---:|
|**d** | 0 | 0.07 | 0.1\* | 0.1 | 0.1 |
|**e** | 0.07 | 0 | 0.1 | 0.1 | 0.1 |
|**f** | 0.1 | 0.1 | 0 | 0.04 | 0.06 |
|**g** | 0.1 | 0.1 | 0.04 | 0 | 0.06 |
|**h** | 0.1 | 0.1 | 0.06 | 0.06 | 0 |
]
.reduce70[\* Note; this is twice the root-to-tip distance.]
]

.pull-bottom[
Any ultrametric tree satisfies the three-point condition (for rooted trees): for any three tips x, y, z, the larger two pairwise distances of D(x, y), D(x,z), D(y,z) will be equal.
]

---

# These distances are _ultrametric_
 
 
.left-column40[
	![Schematic of a phylogenetic tree containing internal nodes a, b, c. Nodes d, e, f, g and h form the tips. The branches of the tree are annotated with numbers that represent the evolutionary distance between species. The distance between the root and tip on all branches is the same. Described at 4:44 in the video recording.](graphics/04-UltrametricTree-1.png)
]
.right-column60[
Distance matrix:
.center[
| | d | e | f | g | h |
|:---:|:---:|:---:|:---:|:---:|:---:|
|**d** | 0 | 0.07 | 0.1 | 0.1 | 0.1 |
|**e** | - | 0 | 0.1 | 0.1 | 0.1 |
|**f** | - | - | 0 | 0.04 | 0.06 |
|**g** | - | - | - | 0 | 0.06 |
|**h** | - | - | - | - | 0 |
]
 
Since this is a symmetric matrix we usually just show half of it...
]

---

# These distances are _ultrametric_
 
 
.left-column40[
	![Schematic of a phylogenetic tree containing internal nodes a, b, c. Nodes d, e, f, g and h form the tips. The branches of the tree are annotated with numbers that represent the evolutionary distance between species. The distance between the root and tip on all branches is the same. Described at 4:44 in the video recording.](graphics/04-UltrametricTree-1.png)
]
.right-column60[
Distance matrix:
.center[
|	| e | f | g | h |
|:---:|:---:|:---:|:---:|:---:|:---:|
|**d** | 0.07 | 0.1 | 0.1 | 0.1 |
|**e** | - | 0.1 | 0.1 | 0.1 |
|**f** | - | - | 0.04 | 0.06 |
|**g** | - | - | - | 0.06 |
]
 
... and only the non-zero entries.
]

---
# The general approach
 
 
![Flow chart illustrating how sequence alignment data or dis/similarity measures are used to calculate and calculate phylogenetic distances. Colours and shapes are used to differentiate different sections of the flowchart, guiding the viewer through each step from left to right. The flowchart begins with Sequence Alignment or Dis/Similarity Measures. These are used to form a distance matrix (D) which is used to select two nodes (x and y) forming a new node z. The distance matrix is updated with the new node z until no further nodes can be formed. Described at 8:20 in the video recording.](graphics/TreeConstruction.drawio.png)

---

# Our distances
 
 
* We get distances from molecular sequences once they have been _aligned_.
* There are various ways to compare aligned sequences to obtain distances:
	- uncorrected "p-distance" -- the proportion of sites that differ between the two sequences;
	- the Jukes-Cantor (JC69) correction, which takes into account of multiple character state changes through time;
	- The Hasegawa-Kishino-Yano (HKY85) model, which also allows for variation in nucleotide frequencies \$\pi\_{A}, \pi\_{C}, \pi\_{G}, \pi\_{T}\$ as well as different transition/transversion rates;
	- and more.

---

# Jukes-Cantor / JC69
 
This model has one single parameter, assuming that the base frequencies are each 25%: \$\pi\_{A}=\pi\_{G}=\pi\_{C}=\pi\_{T}=0.25\$
 
 
The rate matrix looks like this:
 
.image-40[ ![Rate matrix representing the Jukes Cantor model. The matrix has the nucleotides AGCT on both the x and y axis. The substitution rates are identical and represented by the character alpha. Asterisks are used as shorthand for values that make the row sums equal 0. Described at 11:31 in the video recording.](graphics/04-QJC69-1.png) ]
 
.reduce50[where the asterisk is a short-hand to make the row-sums equal 0.]
 
 
Under this model the expected number of substitutions between two sequences with a p-distance of \$p\$ is
$$\hat{d} = \frac{-3}{4}\ln\left(1-\frac{4}{3}p\right)$$

---
# Hasegawa-Kishino-Yano / HKY85
 
This model allows for variation in nucleotide frequencies \$\pi\_{A}, \pi\_{G}, \pi\_{C}, \pi\_{T}\$ as well as different transition/transversion rates using parameter \$\kappa\$: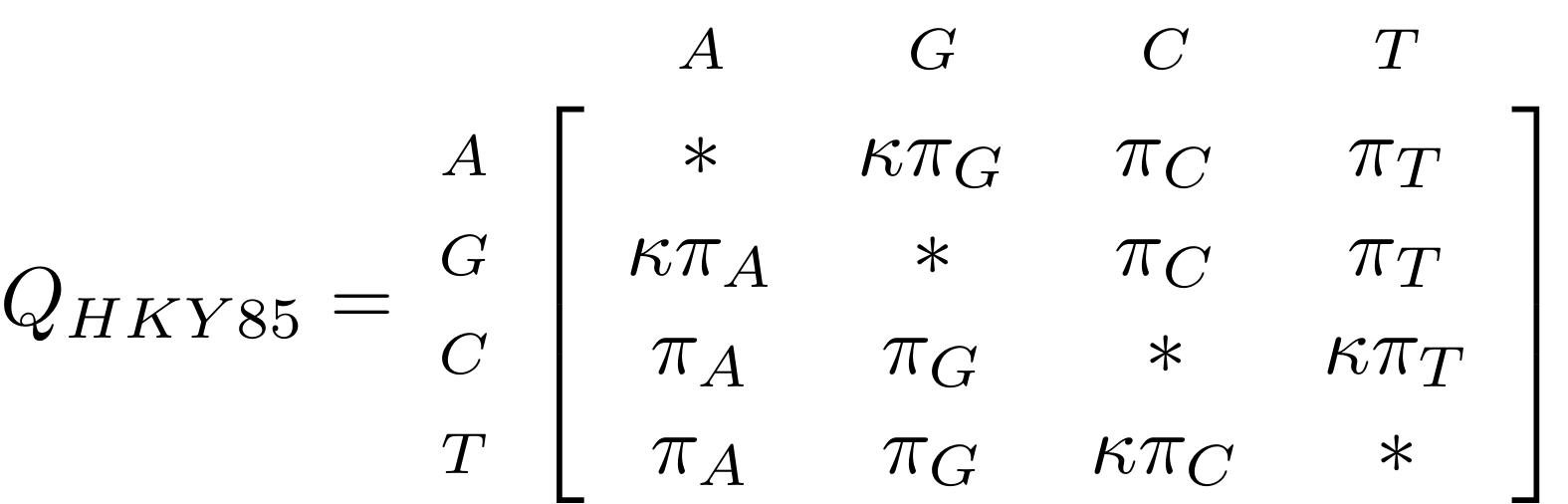
 
 
.image-40[ ![Rate matrix representing the HKY85 model. The matrix has the nucleotides AGCT on both the x and y axis. Variation in nucleotide frequencies πA; πG; πC; πT as well as different transition/transversion rates using parameter kappa. Described at 14:08 in the video recording.](graphics/04-QHKY85-1.png) ]
 
 
This model also allows for a correction to turn relative observed numbers of substitutions between the different bases into expected total number of substitutions between two sequences, but it is much more complex.

---

# From alignment to distances
 
 
.left-column50[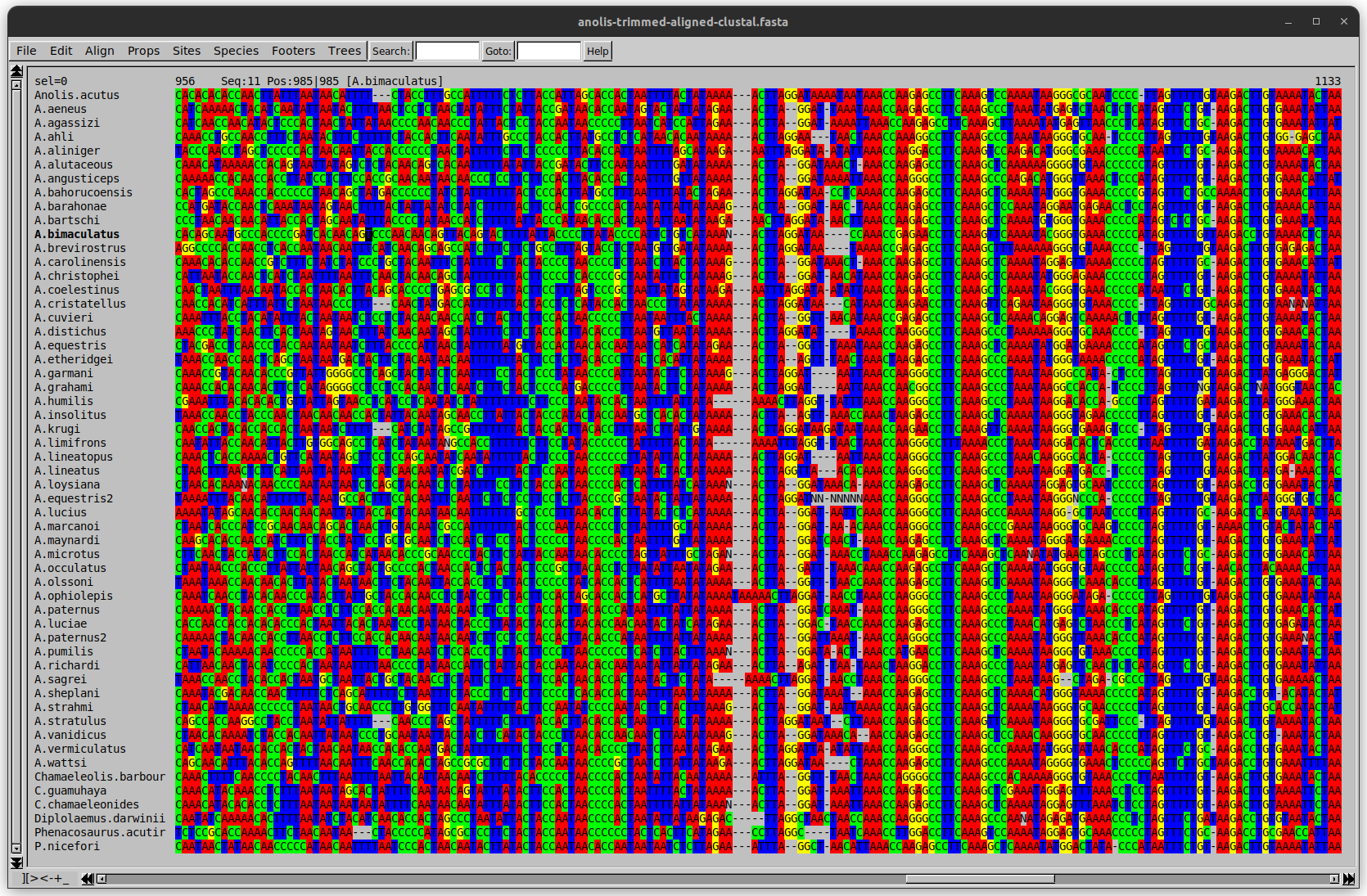
	![Screenshot from the program SeaView showing a multiple sequence alignment of Anolis species. DNA sequences are aligned vertically and nucleotides are colour coded. Aligned sites can be identified by solid lines of colour that run from top to bottom of the image. Full description included in the video recording at 40:06.](graphics/AnolisPartialAlignmentGapsAlignedTidied.png)
]
.right-column50[
	![Figure representing a distance matrix (D) comparing sequences from A. acutus and A. aeneus.](graphics/04-AnolisDistanceMatrixCorner-1.png)
 
 
Once the alignment is complete, each pair of sequences is compared to give an estimated distance between them: this forms the distance matrix for tree building.
]
---
# Example
 
 
_Ultrametric distances_

---
# The true tree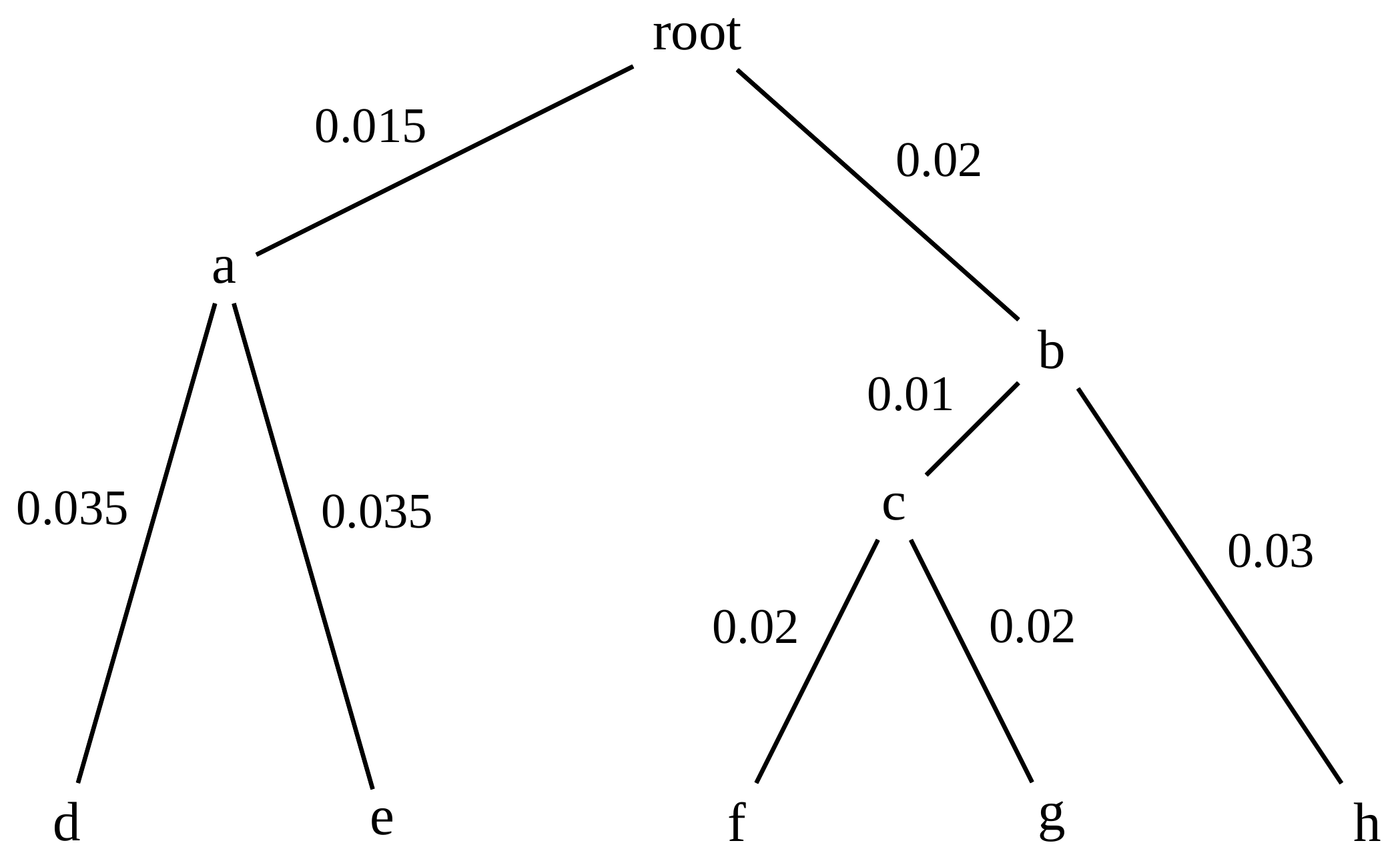
 
 
![Schematic of an ultrametric phylogenetic tree containing internal nodes a, b, c. Nodes d, e, f, g and h form the tips. The branches of the tree are annotated with numbers that represent the evolutionary distance between species. The distance between the root and tip on all branches is the same.](graphics/04-TrueTreeUltrametric-1.png)

---
# Original Distance Matrix
 
 
![Distance matrix representing the evolutionary distance between nodes d, e, f, g and h on a phylogenetic tree.](graphics/04-InitialDistancesUltrametric-1.png)
---
# Original Distance Matrix
 
 
![Distance matrix representing the evolutionary distance between nodes d, e, f, g and h on a phylogenetic tree. The distance between g and f is highlighted in red and has a value of 0.04.](graphics/04-InitialDistancesUltrametric-2.png)
---
 
 
 
 
 
![The letters d, e, f, g and h are equally distributed horizontally. They represent the tips of a phylogenetic tree. Described at 16:08 in the video recording.](graphics/04-TreeBuildStep1-1.png)
---

![The letters d, e, f, g and h are equally distributed horizontally at the bottom of the image. They represent the tips of a phylogenetic tree. An internal node c sits above the tips and is connected to nodes f and g. Described at 16:08 in the video recording.](graphics/04-TreeBuildStep2-1.png)
---
 
 
 
 
 
![The letters d, e, f, g and h are equally distributed horizontally at the bottom of the image. They represent the tips of a phylogenetic tree. An internal node c sits above the tips and is connected to nodes f and g. The distance from f to g via c is highlighted with a red dotted line and annotated with the value 0.04.Described at 16:08 in the video recording.](graphics/04-TreeBuildStep3-1.png)
 
 
The distance between f and g *D(f,g)* is the sum of the branch lengths on the path between them.
---

![The letters d, e, f, g and h are equally distributed horizontally at the bottom of the image. They represent the tips of a phylogenetic tree. An internal node c sits above the tips and is connected to nodes f and g. The distance from f to g via c is highlighted with a red dotted line and annotated with the value 0.04. A blue dotted line represents the distance between f and h with the value 0.06. A green dotted line represents the distance between g and h with the value 0.06. Described at 16:08 in the video recording.](graphics/04-TreeBuildStep4-1.png)
 
 
Similarly the distances *D(f,h)* and *D(g,h)* are the sum of branch lengths.
---

![The letters d, e, f, g and h are equally distributed horizontally at the bottom of the image. They represent the tips of a phylogenetic tree. An internal node c sits above the tips and is connected to nodes f and g. The distance from f to g via c is highlighted with a red dotted line and annotated with the value 0.04. A blue dotted line represents the distance between f and h with the value 0.06. A green dotted line represents the distance between g and h with the value 0.06. A brown line represents the path between c and h with the value 0.08. Described at 16:08 in the video recording.](graphics/04-TreeBuildStep5-1.png)
 
 
Therefore: 
 
$$\mathbf{D(c,h)} = \frac{D(f,h)+D(g,h)-D(f,g)}{2}$$

---
# Forming the next Distance Matrix
 
 
We need to remove columns and rows f and g, and add new column and row c.

.image-75[ ![Distance matrix (D0) representing the evolutionary distance between nodes d, e, f, g on the y axis and e,f, g and h the x axis. Explanation provided at 19:00 in the video recording.](graphics/04-DistanceMatrixMod1-1.png) ]

---
# Forming the next Distance Matrix
 
 
The entries for *D(f,d), D(g,d)* etc get dropped.

.image-75[ ![Distance matrix D1 representing the evolutionary distance between nodes d, e, f, g and c on the y-axis and nodes e, f, g, c and h on the x-axis. Some values have been struck out or replaced with a formula to illustrate how a matrix is sequentially updated during the tree building process. Explanation provided at 19:00 in the video recording.](graphics/04-DistanceMatrixMod3-1.png) ]
 
 
$$D(c,d) = \frac{1}{2}(D(f,d)+D(g,d)-D(f,g)) = \frac{1}{2}(0.1+0.1-0.04) = \mathbf{0.08}$$
---
# Forming the next Distance Matrix
 
 
We fill in the new entries using the formulae below:

.image-75[ ![Distance matrix D1 representing the evolutionary distance between nodes d, e, f, g and c on the y-axis and nodes e, f, g, c and h on the x-axis. Some values have been struck out to illustrate how a matrix is sequentially updated during the tree building. The distances from d to c and e to c are highlighted and are 0.08. Explanation provided at 19:00 in the video recording.](graphics/04-DistanceMatrixMod5-1.png) ]
 
 
$$D(c,h) = \frac{1}{2}(D(f,h)+D(g,h)-D(f,g)) = \frac{1}{2}(0.06+0.06-0.04) = \mathbf{0.04}$$
---
# Forming the next Distance Matrix
 
 
.image-75[ ![Distance matrix D1 representing the evolutionary distance between nodes d, e, f, g and c on the y-axis and nodes e, f, g, c and h on the x-axis. Some values have been struck out to illustrate how a matrix is sequentially updated during the tree building. The distances from d to c and e to c are highlighted and are 0.08. The distance between c and h is highlighted and is 0.04. Explanation provided at 19:00 in the video recording.](graphics/04-DistanceMatrixMod6-1.png) ]
---
# Forming the next Distance Matrix
 
 
Completed new distance matrix:

.image-50[ 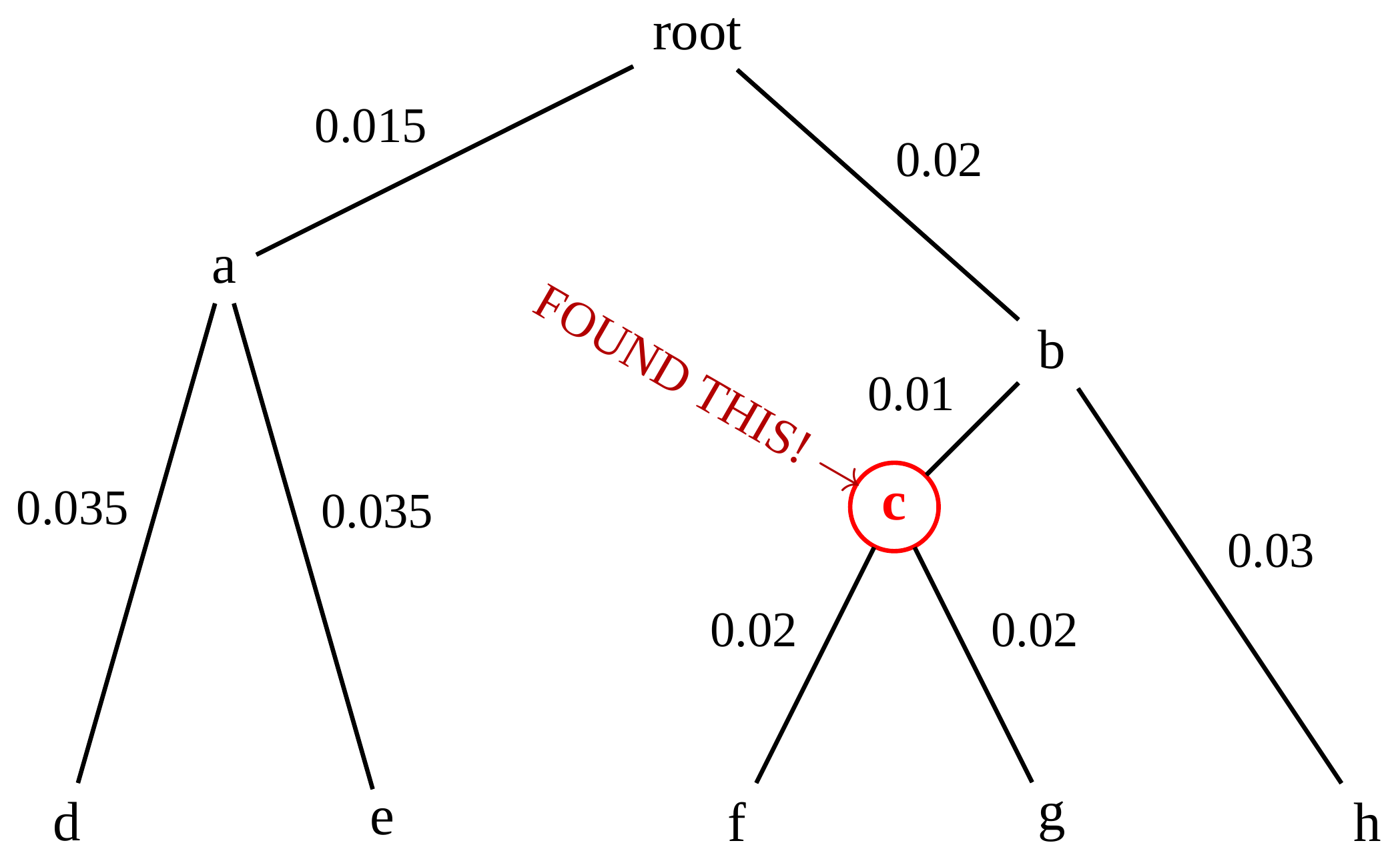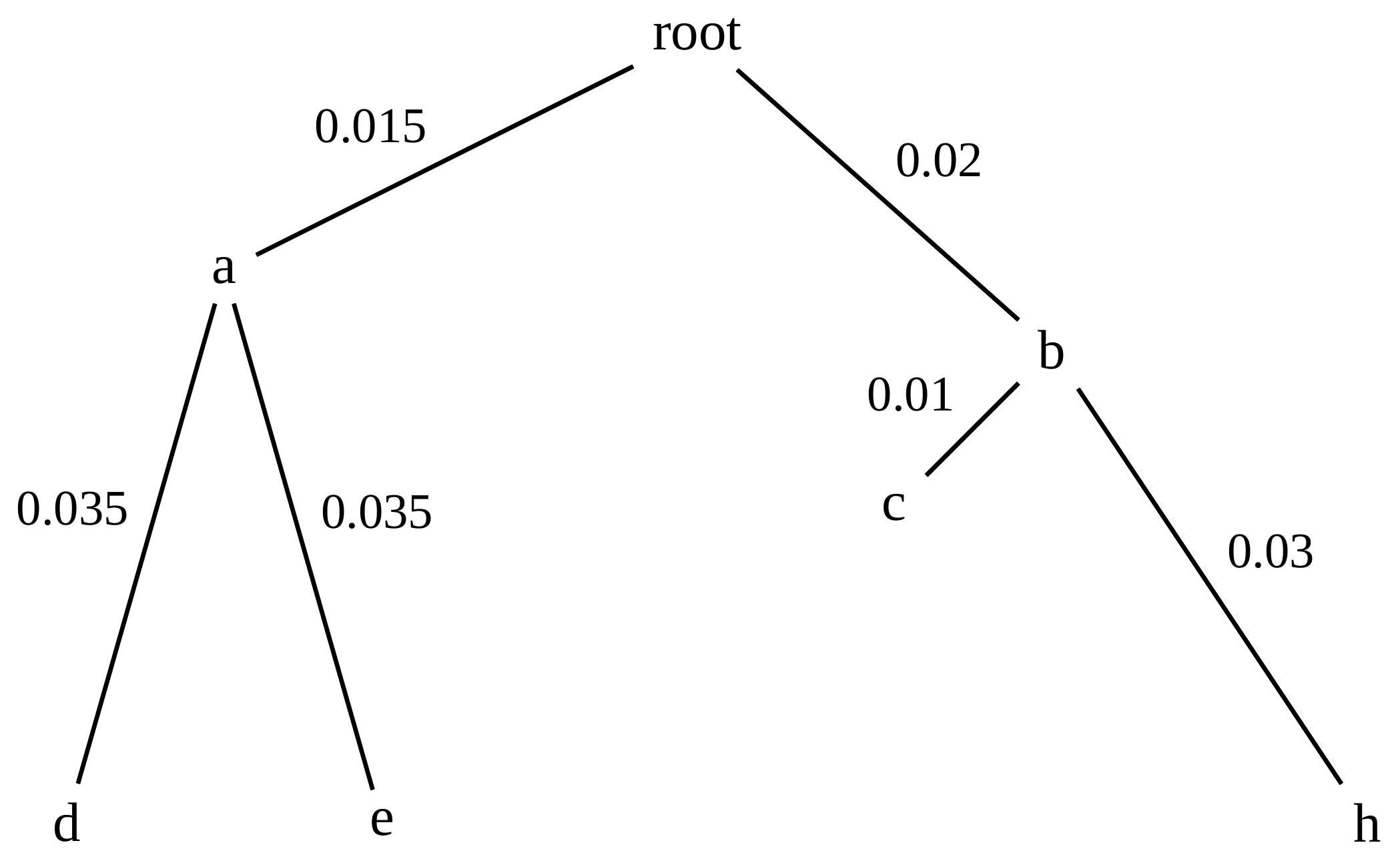![Distance matrix D1 representing the evolutionary distance between nodes d, e, c,  and e, c and h on a phylogenetic tree.](graphics/04-NewDistanceMatrix1-1.png) ]

---

![Schematic of an ultrametric phylogenetic tree containing internal nodes a, b, c. Nodes d, e, f, g and h form the tips. The branches of the tree are annotated with numbers that represent the evolutionary distance between species. The distance between the root and tip on all branches is the same. Node c is circled in red and annotated with the words ‘Found this!’.](graphics/04-FoundC1-1.png)

---

![Schematic of a phylogenetic tree containing internal nodes a and b. Nodes c, d, e, and h form the tips. The branches of the tree are annotated with numbers that represent the evolutionary distance between species. ](graphics/04-FoundC2-1.png)

Now we have reduced the problem by one taxon / sequence: we repeat until we have just two more taxa to join and that will give us the root!

---
# Non-clocklike trees
 
 
*Losing the ultrametric property*
---
# Not perfectly clock-like
 
 
Now suppose this is the _true_ tree relating some species of interest, with actual branch lengths as labelled: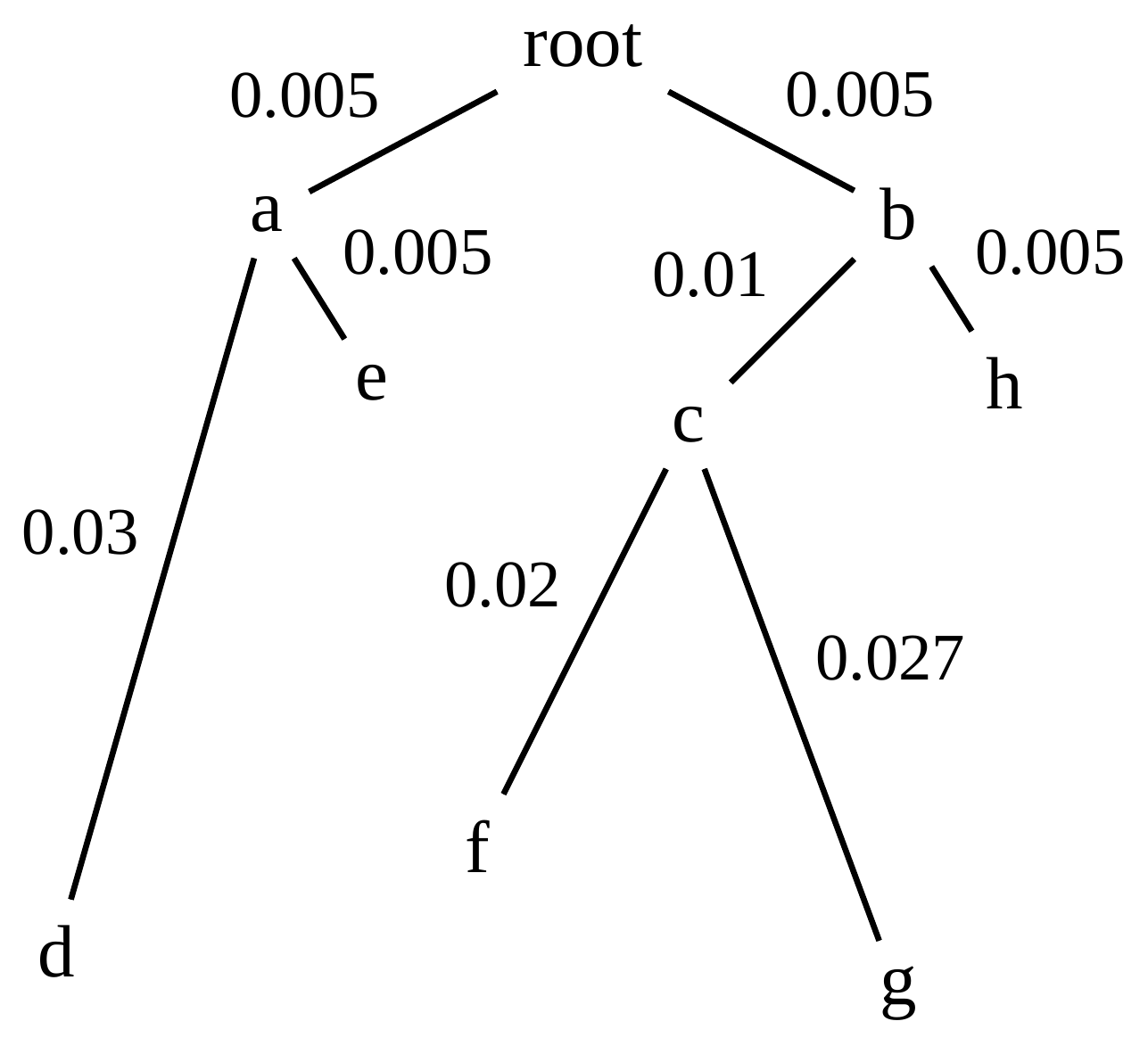
 
 
![Schematic of a rooted non-clocklike phylogenetic tree containing internal nodes a, b, c. Nodes d, e, f, g and h form the tips. The branches of the tree are annotated with numbers that represent the evolutionary distance between species. The distance between the root and tip on all branches is not the same. Description from 21:08 in the video recording.](graphics/04-NonclocklikeTree-1.png)
---
 
 
.left-column40[
	![Schematic of a rooted non-clocklike phylogenetic tree containing internal nodes a, b, c. Nodes d, e, f, g and h form the tips. The branches of the tree are annotated with numbers that represent the evolutionary distance between species. The distance between the root and tip on all branches is not the same. Description from 21:08 in the video recording.](graphics/04-NonclocklikeTree-1.png)
]
.right-column60[
.image-75[ 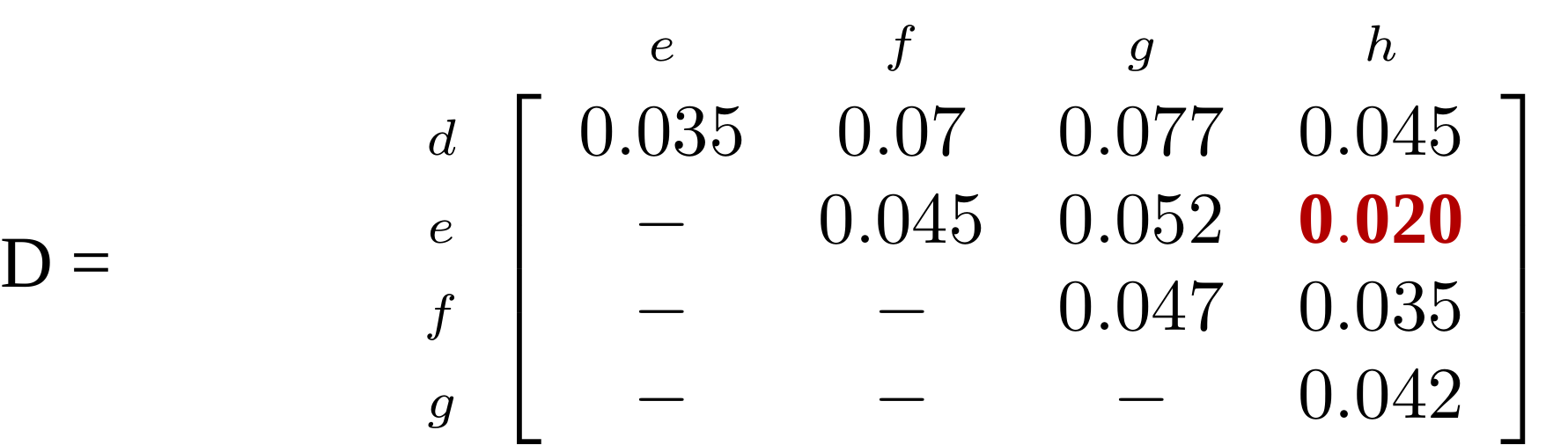![Distance matrix D from a non-clocklike phylogenetic tree comparing evolutionary distances between nodes d, e,f g on the y-axis and e, f, g and h on the x-axis. The smallest distance between e and h is highlighted and is 0.020. Description from 21:08 in the video recording.](graphics/04-NonclocklikeTreeDistances-1.png) ]
 	
The smallest distance doesn't match a true pair of siblings.
]

---
# Neighbo[u]r-Joining
 
 
Neighbo[u]r-Joining solves this problem by accounting for the *net divergence* of node from the rest, so if distances are tree-like, even if they're not ultrametric, it *will* get the tree right.
 
 
The formula for net divergence, with *n* taxa (i.e., an *n* *x* *n* distance matrix) is
 
 
$$r\_{i} = \frac{1}{n-2}\sum\_{j\neq i}D(i,j)$$
 
 
And the adjusted distance becomes
 
 
$$D^{\ast}(i,j) = D(i,j) - r(i) - r(j)$$

---
# Adjusted distance matrix
 
Net divergences:
.center[
| $$i$$ | $$r(i)$$ |
|:---:|:------:|
|	d | 0.075666 |
|	e | 0.050666 |
|	f | 0.065666 |
|	g | 0.072666 |
|	h | 0.047333 |
]
 
Adjusted Distances:
 
.image-50[ ![Adjusted Distance matrix D* from a non-clocklike phylogenetic tree comparing evolutionary distances between nodes d, e,f g on the y-axis and e, f, g and h on the x-axis. The values have been adjusted using the Neighbor-Joining method. Description from 24:03 in the video recording.](graphics/04-NJAdjustedDistances-1.png) ]

---

![Schematic of a rooted non-clocklike phylogenetic tree containing internal nodes a, b, c. Nodes d, e, f, g and h form the tips. The branches of the tree are annotated with numbers that represent the evolutionary distance between species. The distance between the root and tip on all branches is not the same. The paths from d to e via a and f to g via c are highlighted in purple. Description from 24:03 in the video recording](graphics/04-NJTriumphs-1.png)

---
#Realistic data
 
 
*Losing tree-like distances*
---
* Real data are not tree-like in general.
* We should adjust the final branch lengths that are found.
* One criterion is _Minimum Evolution_; this minimises the sum of squared differences ("ordinary least squares"; OLS) between the patristic distances, say _G_, from the tree and the original distances _D_:
 
$$OLS = \sum\_{i,j}(D(i,j) - G(i,j))^{2}$$
 
This assumes that the estimates are independent of each other, which clearly isn't the case as the distances between tips in the tree often share parts of the paths between them.
 
 
.reduce70[ Further reading: Denis and Gascuel: doi.org/10.1016/S0166-218X(02)00285-8. ]

---
# _Anolis_ tree with uncorrected p-distances
 
 
![Screenshot of a phylogenetic tree of Anolis species created in SplitsTree using uncorrected p-distances. The root of the tree is at the centre of the image and branches outward. There are a large number of very short branches near the centre of the tree.The branches are labelled with Anolis species names. Described from 28:44 in the video recording.](graphics/04-AnolisTreeUncorrectedPDistances-1.png)

---
# _Anolis_ tree with JC69 distances
 
 
![Screenshot of a phylogenetic tree of Anolis species created in SplitsTree using the Jukes Cantor model. The root of the tree is at the centre of the image and branches outward. The branches are labelled with Anolis species names. Described from 29:21 in the video recording](graphics/04-AnolisTreeJC69Distances-1.png)

---
# _Anolis_ tree with HKY85 distances
 
 
![Screenshot of a phylogenetic tree of Anolis species created in SplitsTree using the HKY85 model. The root of the tree is at the centre of the image and branches outward. The branches are labelled with Anolis species names. Described from 29:55 in the video recording](graphics/04-AnolisTreeHKY85Distances-1.png)

---
# Limitations
 
 
* A tree-building method will _always give you a tree_, even if the data didn't come from one.
* There is no information on "next best" trees.
* There is no measure of "goodness" for the most part (though you could always quote the least squares error).
* Lastly, there is by default no going back on bad decisions: because NJ is a greedy heuristic, once the tree is finished, we _stop_. Luckily, we have programs like FastTree to do some adjustment!

---

#Thank you!
 
 
_Next - estimating trees from alignments_
---

---

## Thank You!

This material is the result of a collaborative work. Thanks to the [Galaxy Training Network](https://training.galaxyproject.org) and all the contributors!

<div class="contributors-line">
		Authors: <a href="/training-material/hall-of-fame/mcharleston/" class="contributor-badge contributor-mcharleston"><img src="https://avatars.githubusercontent.com/mcharleston?s=36" alt="Michael Charleston avatar" width="36" class="avatar" />
 Michael Charleston</a>
	</div>

</div>

</div>

Tutorial Content is licensed under <a rel="license" href="http://creativecommons.org/licenses/by/4.0/">Creative Commons Attribution 4.0 International License</a>.